A lot of people wonder how to adjust all the controls on the guitar amp or on effect devices to recreate the sound of song xy. Such questions are common in guitar forums all over the internet. Of course it is almost impossible to say which setting someone needs to recreate an authentic sound with his individual gear. Besides, even if you use exactly the same kind of setup with the same setting as on the original song, this does not guarantee to get the same sound because the probably most important sound factor is the playing technique, the old saying “the sound is in his fingers”.
Nevertheless, to know the original setting of a sound can help you to come as close as possible within your playing ability. In the studio, most engineers take photos of amp settings in case a part of the recording has to be fixed with later overdubs, but these pictures almost never get into the public. On Dire Straits’ On Every Street tour (1991/92) however, Mark Knopfler’s then-guitar technician Ron Eve allowed a few interviewers to copy his chart with most settings for the amps and effects. Such a chart appeared in a Mark Knopfler interview in Germany’s Gitarre & Bass magazine, and another one was from the England tour (unfortunately I must admit I downloaded it some years ago but cannot find it anymore).
Ron Eve changed the settings for the two amps and switched between the effect programs for each song. They used two Soldano amps, one is the active amp for a song so that the other amp can be in advance adjusted for the next song. In fact, only the pre-amps are alternated, the power sections of both amps feed a stereo signal into the two Marshall cabinets.
This chart is not really self-explaining, but with some research most parameters can be identified. Here is the chart:
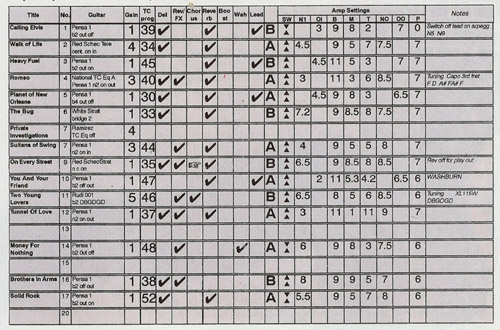
What exactly do all the columns and figures mean?
Title
The title of the song, nothing to add here except that Tunnel of love was not always played. If not, it was replaced by Telegraph Road.
No.
Just the number of the song.
Guitar
This column does not only list the guitar for the song but also the pick-up combinations or control settings. The denotion of the pick-up combinations is a bit inconsistent: while ‘b2’ seems to be ‘second position from bridge’ = bridge & middle, and ‘n2’ for ‘second position from neck’ = neck & middle, on Planet of New Orleans it says ‘b4’ which might be be ‘fourth position from bridge’ = neck & middle (why not ‘n2’ here ?). On Walk of Life it says ‘cent.’ which is center position (bridge & neck), and on On Every Street ‘n c’ should be ‘neck & center’ (the Schecter Strat has three individual switches, so something like ‘n2’ makes less sense here).
In addition to the pick-up combination we find notes like ‘on’, ‘out’, ‘off’, or ‘in’. On the Pensa these should have to do with the active mid boost (avtivated with a push/pull poti, I guess ‘out’ is on, ‘in’ is off). I am not sure what ‘on’ and ‘in’ might stand for, it seems only the tone control is left as a candidate (?). Please make your suggestions using the comment function.
Gain
This might be the gain setting of the pre-amp in the Cornish rack system that was the container for Knopfler’s 19″ rack effects.
TC prog
The TC was the 2290 delay, these numbers should be of the program in which they saved the settings for each song
Del
This should be another delay, presumably the Alesis Quadraverb (or it is the Zoom 9010, see Rev/FX). Here we only find ‘checked’ (on) or not. I suspect this effect had a fixed setting and was just switched on for an additional delay effect.
Rev/FX
Maybe the Zoom 9010, or the Alesis Quadraverb, see Del above.
Reverb
The Yamaha REV 5
Wah
The fixed-psoition wah wah (a Dunlop Cry Baby) was only used for Money for Nothing, it was built into the rack.
Lead
Lead (=overdrive) channel of the Soldano amp, if not checked, the normal channel was used, see below.
(Amp)
The two Soldano SLO 100 amps were denoted with A and B.
Amp Settings (note that the Soldano controls go up to 11)
SW
These arrows correspond to the Bright (upper arrow) and Crunch switches (down should be off, up should be on)
N1 / OI
Gain control of the Normal or Overdrive channel
M / M / T
Bass / middle / treble
MO / OO
Master volume of the Normal or Overdrive channel
P
Presence control
Notes
It seems on Calling Elvis the overdrive channel was switched to the normal channel during an arpeggio (which?) , N5 and N9 can be the setting of maybe normal gain and normal master
XL 115W is the string set for the red Pensa on Two Young Lovers.
Maybe a black-out, but I have no idea which Washburn can be meant.
Some general notes
As said there were one or two more of these charts around from other concerts. What is striking is the high setting of the bass control, mind he uses two closed 4 x 12″ cabinets which have normally plenty of bass.

29 thoughts on “Mark Knopfler’s Amp and Effect Settings on the On Every Street tour”
Hi,
did he use his Pensa on the outro of Romeo & Juliet? I never saw that he played the outro on the OES-tour did they cut the DVDs?
No, they didn’t edit the DVDs. The answer is: he did in 1991, he did not in 1992. This chart is from 1991.
I think that in Calling Elvis amp swiched from overdrive to normal is in the end of the song:
Is it Mark (overdrive), Franklin pedal steel, Mark (clean) yms.
Ingo, after a nice cup of tea this morning I got a eureka moment .. I think the b in eg b2 is n2 with the boost so simply to distinguish between “n2” and “n2 with the boost” he’s written b2 and maybe as a second aid he’s kept the out/in note as second prompt. Tunnel of Love and R&J has the n2 and out so maybe the out is something else entirely?
..just to add b2 and n2 are the neck/middle combo as mark used that more on the pensa than he does on the strats. In Planet of New Orleans he starts with b4 and uses b2 for the fills during verses.
What’s interesting here is that Mark nicked the soldanos for his first home studio in this picture the labels scene during On Every Street on the Soldano are still there, with this one marked with an A! http://www.guyfletcher.co.uk/diaries/Ragpickerstudiodiaryfolder/sdimages/moregain.jpg
Hi,
a long time ago, I found this picture on a guitarpage. It is from 2001 and you can see 2 Soldanos: http://img84.exs.cx/img84/9798/Knoplerrig2001.jpg
Re: no. 6, the Soldano in Mark’s home studio: The amp on top is a rare 1966 Marshall JTM 45. As used in the recording of the song ‘Brothers in Arms’ (with a Les Paul).
http://www.guyfletcher.co.uk/diaries/Ragpickerstudiodiaryfolder/sdimages/marshall.jpg
The ‘off’ referred to in the columns is the tone control as in ‘on’ or ‘off’ Mark generally uses the tone at these start points and doesn’t usually vary them in playing.
‘in’ and ‘out’ refer to the pull switch, so ‘on’ and ‘in’ mean tone is ‘on’ and the switch is in the off position or ‘in’
‘b’ means bridge and ‘n’ is neck so, yes, n2 is the second switch setting from the neck position.
Gain was indeed the preamp setting on the Cornish rack.
Washburn referred to the Washburn bass that John Illsley played on You and Your Friend. It was reminder for the drum tech to hand it to him for this song!
on “on the night” you can clearly see John Illsley playing his Fander Jazz bass on “You and your friend”, not the washburn bass
Hi,
This is not from Nov 7 show in Brisbane of the OES tour. They didn’t play Tunnel, but did play Telegrah Road. Though it might be useful at some point…
Good work
Dan
Weird that Local Hero doesn’t appear on this list. Did they only play it in 1992?
Thank you very much for sharing. Your information always proves to be useful. I think your post is suitable for everyne, who is interested in valuable resources. I will keep following your posts.
Thank you for your contribution to my forex trading experience and helping traders like me get started. It’s very educating. I am very new to forex trading and I am looking forward to learn from your next entry.
Why did they change the TC program even when there was no delay used (for example on Heavy Fuel, Sultans, Two Young Lovers and Money For Nothing)?
See the notes again, I presume the column ‘Del’ does not refer to the TC but to another delay.
I think in and off means out-of-phase(off) and in-of-phase(on)
He usually uses the strat for sultans of swing
Hi,
afaik it was said that the TC 2290 was midi’d to the other effects, so maybe they only switched the programm on the TC (even if the delay of the 2290 was bypassed) to change the presets of the other effects. Otherwise they would have had to change the presets after each song on all FX units. That would explain why Del is sometimes checked and sometimes not.
The foods that you dieting 6 pack abs can” Lose ten pounds while eating chocolate cake! Yet another option is to dieting 6 pack abs eat less from the main course.
Hi Ingo,
Do you have any information on the tubes that used on Mark’s SLO?
or any mods are specifically designed for Mark?
Thanks
SOrry, no info on the tubes. I heard that the amps were modified to split the pre amps and power amps to allow the A/B operation of the two pre amps into both power amps.
lookie here
i don’t get why lead is of on BIA MFN and Solid Rock. You can clearly hear the guitar has overdrive, so how does it get distortion if not with the overdrive channel?
The answer is pretty simple. The Soldano SLO 100 has got a clean and a lead channel. There is a switch that lets you boost the clean channel (the so called crunch mode). Turning up the gain control leads to a overdriven sound then. Some players prefer the crunch mode over the lead channel. Don’t forget that he had a EMG SPC mid boost in his Pensa-Suhr MK1, which was activated in all the three songs you mentioned.
thanx, I looked on google and some SLO100 do have these bright and crunch switches, but some others don’t. Do you know why not all SLO100s have these two switches? I own a soldano reverb-o-sonic and unfortunately mine does not have these!
i meant “lead is off”
Regarding the notes on ‘out’, ‘on’, ‘in’, ‘off’: ‘Out’ and ‘In’ are refering to the push-pull tone-control that activated the EMG SPC in Mark’s Pensa Suhr MK 1. From what I heard there was no way to set the gain of the mid boost. So if you pull the tone-control you get the full mid-boost, there would be no way to set it lower or higher. ‘on’ and ‘off’ probably refer to the tone-control. Either it was on ’10’ (‘on’) or it was rolled off (obviously ‘off’). That would be the only thing that makes sense to me. Maybe they had a little mark or something similiar on the tone-control, so that the guitar-tech could set it on the same spot every time.
what about the Chorus column Ingo?
Trulife Distribution – Nutrition Distribution helps our clients achieve success in a complex, competitive retail environment. Our team of nutrition industry experts takes care of everything from importation compliance to marketing, sales and distribution at the ground level. There is no need to navigate the complicated intricacies of the American market when we have already done the work. Let us use our experience to expand your brand and put your product into the hands of American consumers. https://trulifedist.com/